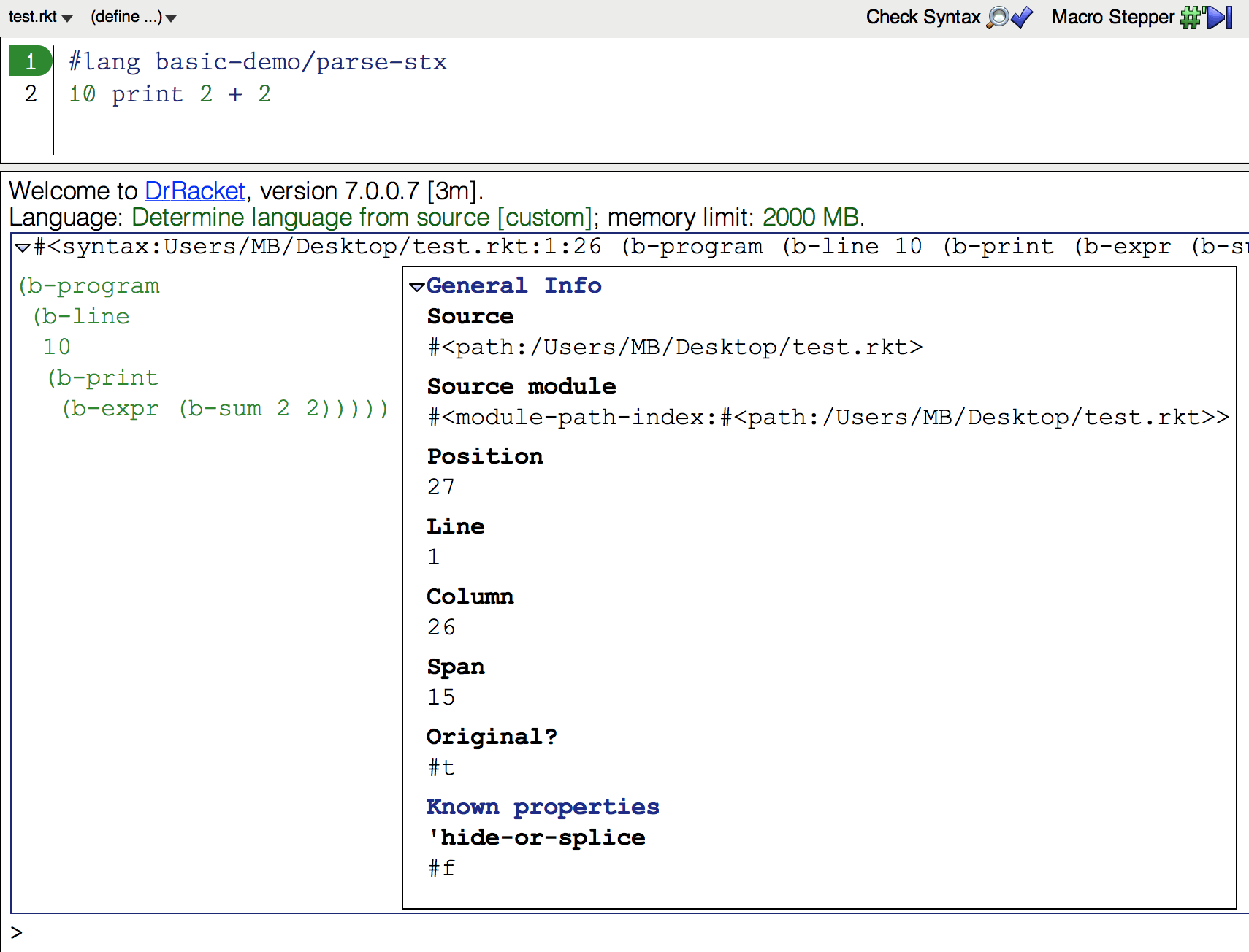
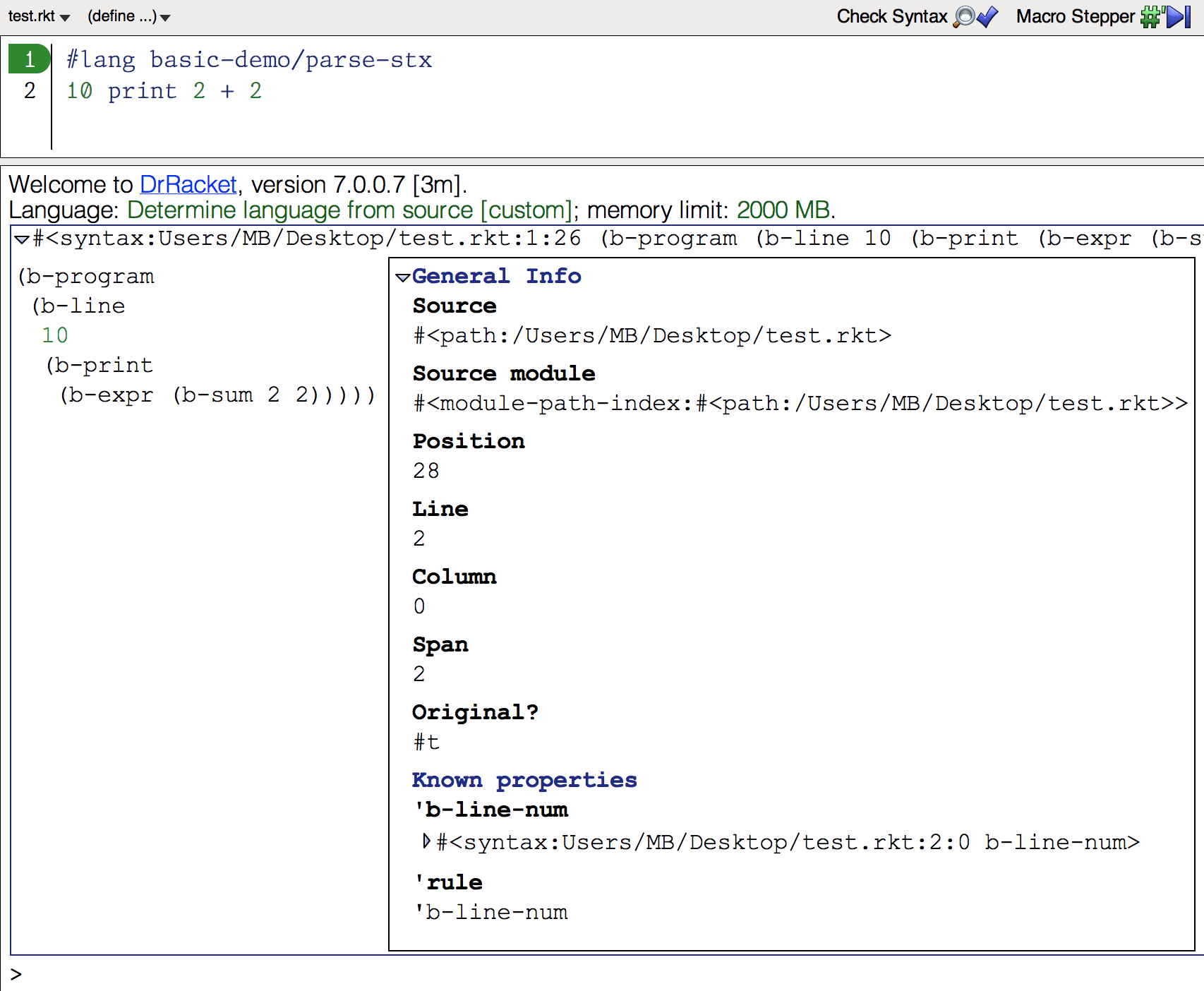
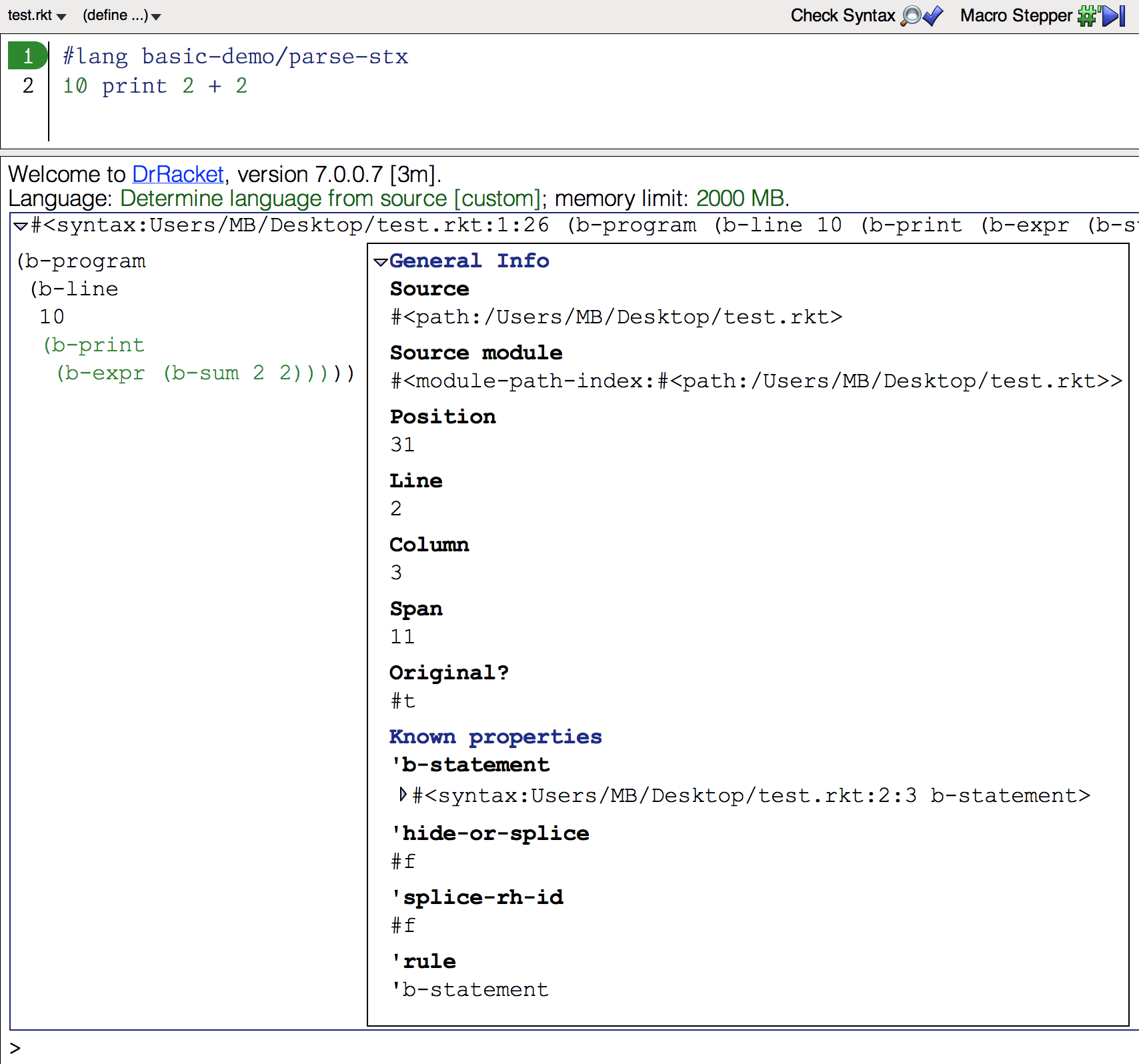
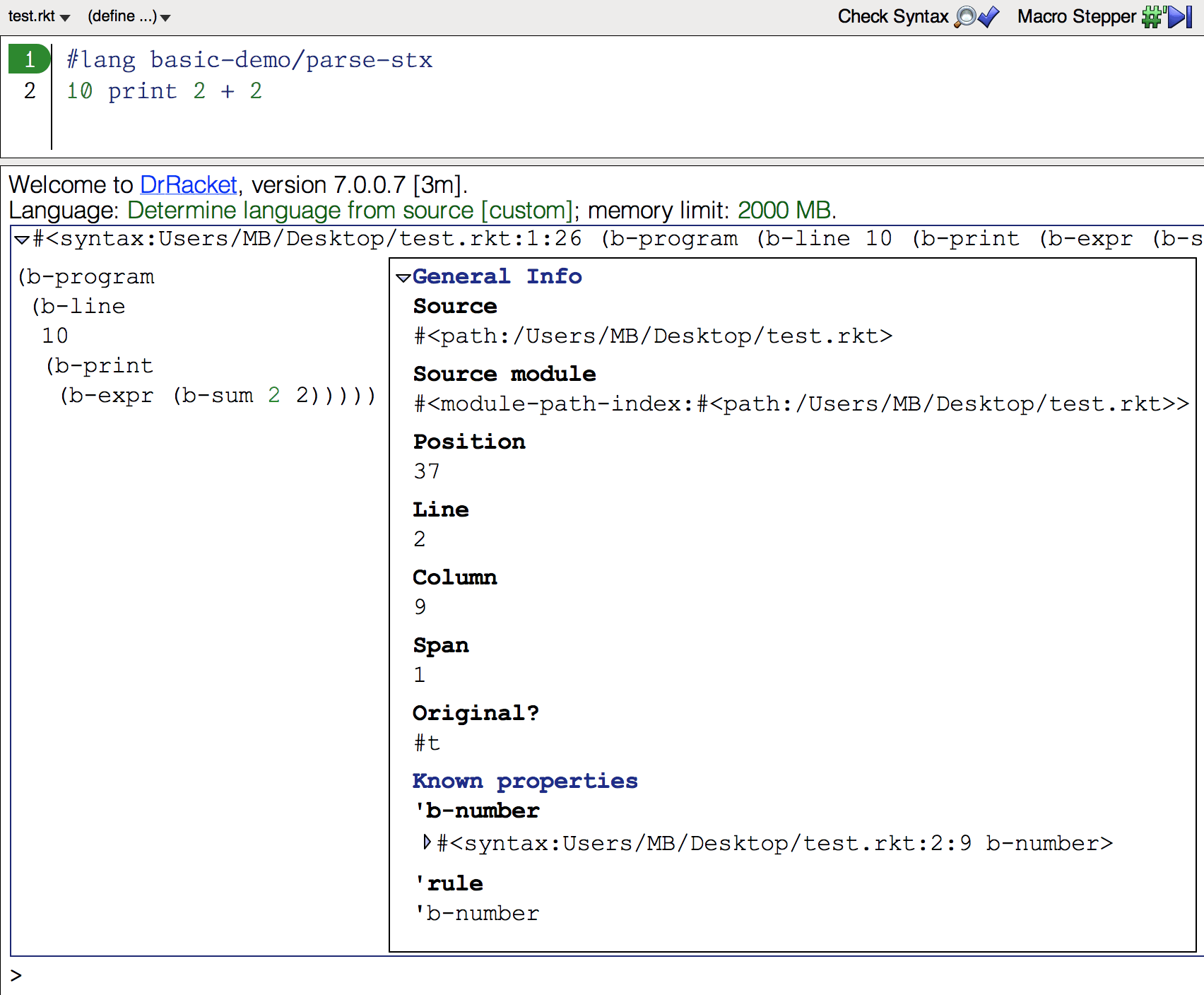
Beautiful Racket / tutorials
- 1 intro
- 2 specification and setup
- 3 the syntax colorer
- 4 better line errors
- 5 variables and input
- 6 expressions
- 7 conditionals
- 8 subroutines and loops
- 9 recap
- 10 source listing
- #lang basic-demo-2
10 let x = 42
20 y = 24
30 print x + y1 2 3 4
#lang basic-demo-2 10 let x = 42 20 y = 24 30 print x + y
- #lang basic-demo-2
10 print x ; y ; z1 2
#lang basic-demo-2 10 print x ; y ; z
basic/expander.rkt
#lang br/quicklang
(require "struct.rkt" "run.rkt" "elements.rkt")
(provide (rename-out [b-module-begin #%module-begin])
(all-from-out "elements.rkt"))
(define-macro (b-module-begin (b-program LINE ...))
(with-pattern
([((b-line NUM STMT ...) ...) #'(LINE ...)]
[(LINE-FUNC ...) (prefix-id "line-" #'(NUM ...))])
#'(#%module-begin
LINE ...
(define line-table
(apply hasheqv (append (list NUM LINE-FUNC) ...)))
(void (run line-table)))))
(require "struct.rkt" "run.rkt" "elements.rkt")
(provide (rename-out [b-module-begin #%module-begin])
(all-from-out "elements.rkt"))
(define-macro (b-module-begin (b-program LINE ...))
(with-pattern
([((b-line NUM STMT ...) ...) #'(LINE ...)]
[(LINE-FUNC ...) (prefix-id "line-" #'(NUM ...))])
#'(#%module-begin
LINE ...
(define line-table
(apply hasheqv (append (list NUM LINE-FUNC) ...)))
(void (run line-table)))))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #lang br/quicklang (require "struct.rkt" "run.rkt" "elements.rkt") (provide (rename-out [b-module-begin #%module-begin]) (all-from-out "elements.rkt")) (define-macro (b-module-begin (b-program LINE ...)) (with-pattern ([((b-line NUM STMT ...) ...) #'(LINE ...)] [(LINE-FUNC ...) (prefix-id "line-" #'(NUM ...))]) #'(#%module-begin LINE ... (define line-table (apply hasheqv (append (list NUM LINE-FUNC) ...))) (void (run line-table))))) |
basic/lexer.rkt
#lang br
(require brag/support)
(define-lex-abbrev digits (:+ (char-set "0123456789")))
(define-lex-abbrev reserved-terms (:or "print" "goto" "end" "+"
":" ";" "let" "=" "input"))
(define basic-lexer
(lexer-srcloc
["\n" (token 'NEWLINE lexeme)]
[whitespace (token lexeme #:skip? #t)]
[(from/stop-before "rem" "\n") (token 'REM lexeme)]
[reserved-terms (token lexeme lexeme)]
[(:seq alphabetic (:* (:or alphabetic numeric "$")))
(token 'ID (string->symbol lexeme))]
[digits (token 'INTEGER (string->number lexeme))]
[(:or (:seq (:? digits) "." digits)
(:seq digits "."))
(token 'DECIMAL (string->number lexeme))]
[(:or (from/to "\"" "\"") (from/to "'" "'"))
(token 'STRING
(substring lexeme
1 (sub1 (string-length lexeme))))]))
(provide basic-lexer)
(require brag/support)
(define-lex-abbrev digits (:+ (char-set "0123456789")))
(define-lex-abbrev reserved-terms (:or "print" "goto" "end" "+"
":" ";" "let" "=" "input"))
(define basic-lexer
(lexer-srcloc
["\n" (token 'NEWLINE lexeme)]
[whitespace (token lexeme #:skip? #t)]
[(from/stop-before "rem" "\n") (token 'REM lexeme)]
[reserved-terms (token lexeme lexeme)]
[(:seq alphabetic (:* (:or alphabetic numeric "$")))
(token 'ID (string->symbol lexeme))]
[digits (token 'INTEGER (string->number lexeme))]
[(:or (:seq (:? digits) "." digits)
(:seq digits "."))
(token 'DECIMAL (string->number lexeme))]
[(:or (from/to "\"" "\"") (from/to "'" "'"))
(token 'STRING
(substring lexeme
1 (sub1 (string-length lexeme))))]))
(provide basic-lexer)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | #lang br (require brag/support) (define-lex-abbrev digits (:+ (char-set "0123456789"))) (define-lex-abbrev reserved-terms (:or "print" "goto" "end" "+" ":" ";" "let" "=" "input")) (define basic-lexer (lexer-srcloc ["\n" (token 'NEWLINE lexeme)] [whitespace (token lexeme #:skip? #t)] [(from/stop-before "rem" "\n") (token 'REM lexeme)] [reserved-terms (token lexeme lexeme)] [(:seq alphabetic (:* (:or alphabetic numeric "$"))) (token 'ID (string->symbol lexeme))] [digits (token 'INTEGER (string->number lexeme))] [(:or (:seq (:? digits) "." digits) (:seq digits ".")) (token 'DECIMAL (string->number lexeme))] [(:or (from/to "\"" "\"") (from/to "'" "'")) (token 'STRING (substring lexeme 1 (sub1 (string-length lexeme))))])) (provide basic-lexer) |
basic/parser.rkt
#lang brag
b-program : [b-line] (/NEWLINE [b-line])*
b-line : b-line-num [b-statement] (/":" [b-statement])* [b-rem]
@b-line-num : INTEGER
@b-statement : b-end | b-print | b-goto | b-let | b-input
b-rem : REM
b-end : /"end"
b-print : /"print" [b-printable] (/";" [b-printable])*
@b-printable : STRING | b-expr
b-goto : /"goto" b-expr
b-let : [/"let"] b-id /"=" (b-expr | STRING)
b-input : /"input" b-id
@b-id : ID
b-expr : b-sum
b-sum : b-number (/"+" b-number)*
@b-number : INTEGER | DECIMAL | b-id
b-program : [b-line] (/NEWLINE [b-line])*
b-line : b-line-num [b-statement] (/":" [b-statement])* [b-rem]
@b-line-num : INTEGER
@b-statement : b-end | b-print | b-goto | b-let | b-input
b-rem : REM
b-end : /"end"
b-print : /"print" [b-printable] (/";" [b-printable])*
@b-printable : STRING | b-expr
b-goto : /"goto" b-expr
b-let : [/"let"] b-id /"=" (b-expr | STRING)
b-input : /"input" b-id
@b-id : ID
b-expr : b-sum
b-sum : b-number (/"+" b-number)*
@b-number : INTEGER | DECIMAL | b-id
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #lang brag b-program : [b-line] (/NEWLINE [b-line])* b-line : b-line-num [b-statement] (/":" [b-statement])* [b-rem] @b-line-num : INTEGER @b-statement : b-end | b-print | b-goto | b-let | b-input b-rem : REM b-end : /"end" b-print : /"print" [b-printable] (/";" [b-printable])* @b-printable : STRING | b-expr b-goto : /"goto" b-expr b-let : [/"let"] b-id /"=" (b-expr | STRING) b-input : /"input" b-id @b-id : ID b-expr : b-sum b-sum : b-number (/"+" b-number)* @b-number : INTEGER | DECIMAL | b-id |
basic/expander.rkt
#lang br/quicklang
(require "struct.rkt" "run.rkt" "elements.rkt")
(provide (rename-out [b-module-begin #%module-begin])
(all-from-out "elements.rkt"))
(define-macro (b-module-begin (b-program LINE ...))
(with-pattern
([((b-line NUM STMT ...) ...) #'(LINE ...)]
[(LINE-FUNC ...) (prefix-id "line-" #'(NUM ...))]
[(VAR-ID ...) (find-unique-var-ids #'(LINE ...))])
#'(#%module-begin
(define VAR-ID 0) ...
LINE ...
(define line-table
(apply hasheqv (append (list NUM LINE-FUNC) ...)))
(void (run line-table)))))
(begin-for-syntax
(require racket/list)
(define (find-unique-var-ids line-stxs)
(remove-duplicates
(for/list ([stx (in-list (stx-flatten line-stxs))]
#:when (syntax-property stx 'b-id))
stx)
#:key syntax->datum)))
(require "struct.rkt" "run.rkt" "elements.rkt")
(provide (rename-out [b-module-begin #%module-begin])
(all-from-out "elements.rkt"))
(define-macro (b-module-begin (b-program LINE ...))
(with-pattern
([((b-line NUM STMT ...) ...) #'(LINE ...)]
[(LINE-FUNC ...) (prefix-id "line-" #'(NUM ...))]
[(VAR-ID ...) (find-unique-var-ids #'(LINE ...))])
#'(#%module-begin
(define VAR-ID 0) ...
LINE ...
(define line-table
(apply hasheqv (append (list NUM LINE-FUNC) ...)))
(void (run line-table)))))
(begin-for-syntax
(require racket/list)
(define (find-unique-var-ids line-stxs)
(remove-duplicates
(for/list ([stx (in-list (stx-flatten line-stxs))]
#:when (syntax-property stx 'b-id))
stx)
#:key syntax->datum)))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | #lang br/quicklang (require "struct.rkt" "run.rkt" "elements.rkt") (provide (rename-out [b-module-begin #%module-begin]) (all-from-out "elements.rkt")) (define-macro (b-module-begin (b-program LINE ...)) (with-pattern ([((b-line NUM STMT ...) ...) #'(LINE ...)] [(LINE-FUNC ...) (prefix-id "line-" #'(NUM ...))] [(VAR-ID ...) (find-unique-var-ids #'(LINE ...))]) #'(#%module-begin (define VAR-ID 0) ... LINE ... (define line-table (apply hasheqv (append (list NUM LINE-FUNC) ...))) (void (run line-table))))) (begin-for-syntax (require racket/list) (define (find-unique-var-ids line-stxs) (remove-duplicates (for/list ([stx (in-list (stx-flatten line-stxs))] #:when (syntax-property stx 'b-id)) stx) #:key syntax->datum))) |
basic/misc.rkt
#lang br
(require "struct.rkt")
(provide b-rem b-print b-let b-input)
(define (b-rem val) (void))
(define (b-print . vals)
(displayln (string-append* (map ~a vals))))
(define-macro (b-let ID VAL) #'(set! ID VAL))
(define-macro (b-input ID)
#'(b-let ID (let* ([str (read-line)]
[num (string->number (string-trim str))])
(or num str))))
(require "struct.rkt")
(provide b-rem b-print b-let b-input)
(define (b-rem val) (void))
(define (b-print . vals)
(displayln (string-append* (map ~a vals))))
(define-macro (b-let ID VAL) #'(set! ID VAL))
(define-macro (b-input ID)
#'(b-let ID (let* ([str (read-line)]
[num (string->number (string-trim str))])
(or num str))))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #lang br (require "struct.rkt") (provide b-rem b-print b-let b-input) (define (b-rem val) (void)) (define (b-print . vals) (displayln (string-append* (map ~a vals)))) (define-macro (b-let ID VAL) #'(set! ID VAL)) (define-macro (b-input ID) #'(b-let ID (let* ([str (read-line)] [num (string->number (string-trim str))]) (or num str)))) |
basic/expr.rkt
#lang br
(provide b-sum b-expr)
(define (b-sum . vals)
(if (= 1 (length vals))
(car vals)
(apply + vals)))
(define (b-expr expr)
(if (integer? expr) (inexact->exact expr) expr))
(provide b-sum b-expr)
(define (b-sum . vals)
(if (= 1 (length vals))
(car vals)
(apply + vals)))
(define (b-expr expr)
(if (integer? expr) (inexact->exact expr) expr))